Research
We focus on the fundamental physics of flow and deformation in porous media. Our goal is to bridge the controlling mechanisms rooted at the microscale to the emergent behaviors observed at the macroscale. A core part of our activities is directed towards devising non-classical algorithms and experimental imaging techniques that probe microscale processes and translate useful insights into macroscale information. Our interests are driven by applications of porous media in energy and the environment. They include subsurface technologies such as CO2 storage, geothermal energy, natural gas, groundwater remediation, as well as manufactured devices such as fuel cells and batteries.
Specific research areas include:
- Multiscale algorithms for microscale fluid and solid mechanics
- Preconditioners and reduced-order models for fracture mechanics
- Pore network models for reliable simulation of solute transport
- Linear and nonlinear solvers for contact mechanics
- Ostwald ripening of bubble populations inside porous media
- Geomaterials characterization through multiresolution imaging
- Hybrid computing to bridge microscale and macroscale physics
Multiscale algorithms for microscale fluid and solid mechanics
Fluid flow and mechanical deformation in porous media is governed by fundamental processes that occur at the scale of individual grains and pores that make up their microstructure. Microscale models can simulate such processes in great detail and establish a link between small-scale physics and large-scale behavior. The understanding that results from probing this link can improve current macroscopic descriptions of flow and mechanics in porous media. From an engineering viewpoint, microscale models are useful for computing material properties, optimizing flow or geometry, and quantifying uncertainty in geological applications. To accomplish any of these tasks, a significant amount of computation is required. Our goal is to design multiscale algorithms that are efficient, accurate, and scalable on parallel machines. We place special emphasis on the ability of algorithms to estimate and control their prediction errors. The end result is a reliable engineering tool applicable to a wide range of practical problems from CO2 storage, subsurface energy production, to designing fuel-cell and battery components.
References:
Mehmani & Tchelepi (2018),
Mehmani & Tchelepi (2019),
Guo, Mehmani, Tchelepi (2019)
Mehmani et al. (2021)
Multiscale simulation of two-phase drainage (Mehmani & Tchelepi, 2019).
Preconditioners and reduced-order models for fracture mechanics
When a porous material is subjected to mechanical, thermal, or hydraulic loading it develops fractures within its microstructure. These fractures emerge out of the coalescence of numerous smaller cracks that nucleate at various points throughout the specimen. Understanding the failure patterns and thresholds are important in designing safer operational protocols for subsurface energy (H2) storage or waste (CO2) disposal and manufacturing lightweight high-strength materials for airplanes, buildings, and biomedical devices. However, the computations needed to obtain such information is often prohibitively expensive. Our goal is, therefore, to develop both multiscale preconditioners that speed up high-fidelity direct numerical simulations and reduced-order models that capitalize on basic insights about how cracks nucleate and grow to enable rapid optimization or uncertainty quantification.
References:
Li & Mehmani (2023),
Mehmani & Li (2023),
Khan et al. (2024)
Preconditioner-accelerated simulation of brittle failure in bone (Li & Mehmani, in review). 3D image courtesy of Amelie Sas at KU Leuven.
Pore network models for reliable simulation of solute transport
Network simulation of advection dominated particle transport (Mehmani & Tchelepi, 2017)
Solute transport is relevant to several applications such as groundwater remediation and CO2 storage in the subsurface as well as drug delivery in microfluidic devices. We have developed pore network models that can simulate transport in the presence or absence of chemical reactions. Network models are a class of microscale models that are approximate in nature. Their approximation is reflected in a simplified representation of the microstructure and the physics. As a result, network computations are very fast, often by orders of magnitude compared to higher fidelity methods (e.g., CFD). However, they are not always reliable as they cannot estimate or control prediction errors. Traditional network models of solute transport can incur large errors, which tend to be highest when molecular diffusion is weak. Our networks overcome such limitations through a mathematical reformulation of the governing equations and a more accurate geometric representation of the microstructure. While the ability to estimate or control errors remains elusive (inherent to all pore networks), we have established empirical error bounds that ensure reliable application of the networks to new problems. Compared to high-fidelity CFD, our network models yield predictions within 10% error at O(103-4) times the speed, openning the door to rapid engineering and control of solute transport in porous media.
References:
Mehmani & Tchelepi (2017),
Oostrom, Mehmani, et al. (2016),
Mehmani & Balhoff (2015a),
Mehmani & Balhoff (2015b),
Yang, Mehmani, et al. (2015),
Mehmani & Balhoff (2014)
Linear and nonlinear solvers for contact mechanics
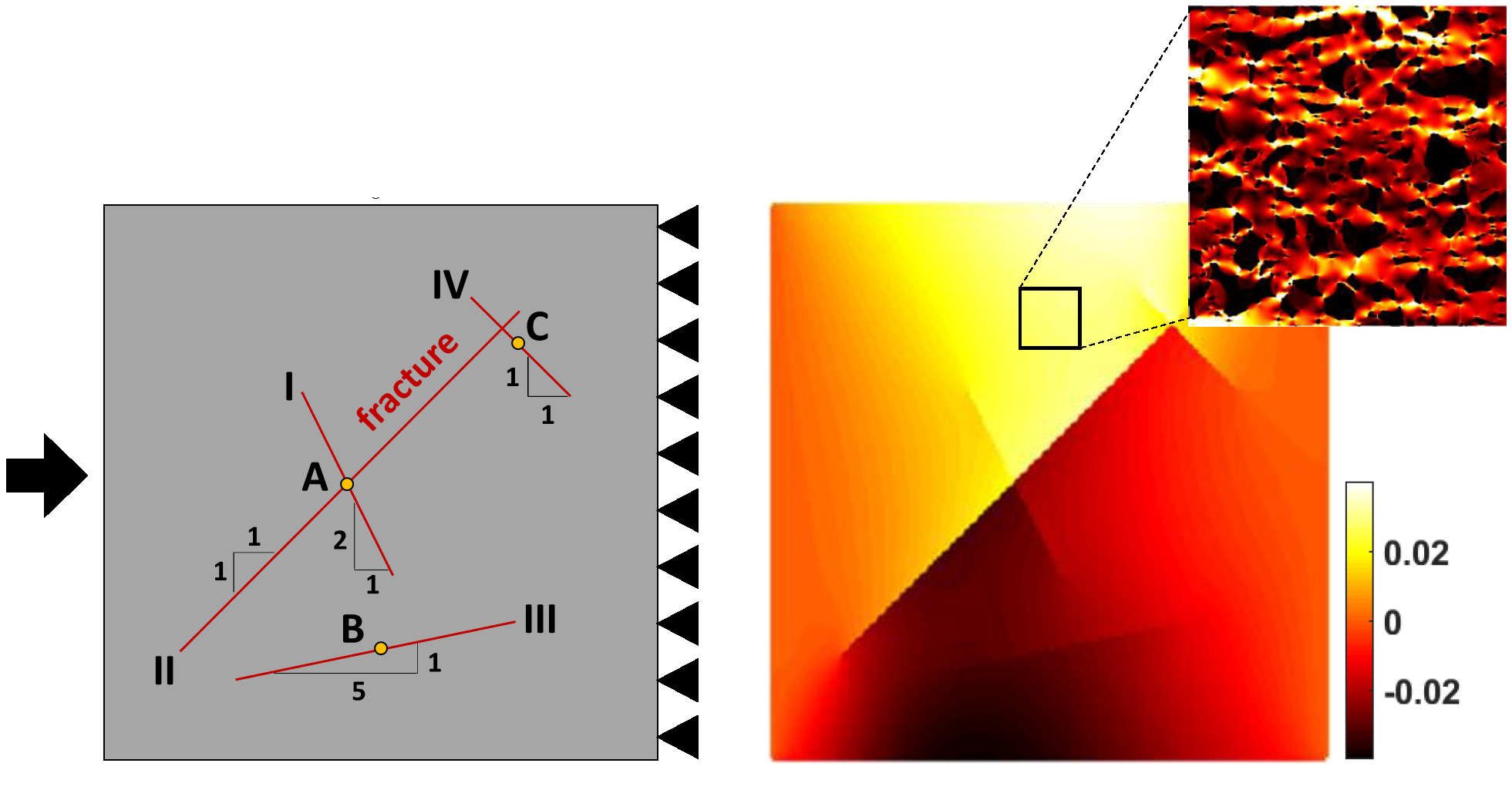
Simulation of mechanical deformation in a fractured domain (Mehmani et al, 2021a)
Contacts are ubiquitous in porous materials. At large scales, contacts appear as internal surfaces of discontinuity, or fractures, within a porous medium often described as a continuum. At small scales, contacts take the form of microcracks or fissures between individual grains or minerals making up the porous medium. In subsurface applications, contacts provide preferential flow paths for in-situ fluids, which can either boost energy recovery (e.g., geothermal) or pose leakage risks for sequestered waste (e.g., nuclear, CO2). In batteries, contacts or cracks reduce the device lifespan by inhibiting the flow of charge through the electrodes. Computational models provide a reliable way to engineer these systems, but the underlying mathematical equations pose significant numerical challenges. Our goal is to design new discretization schemes and linear/nonlinear solvers that can rapidly and robustly solve these equations. The implications extend to a wide range of problems and scales where contacts and fractures are important.
References:
Mehmani et al. (2021a),
Mehmani et al. (2021b)
Ostwald ripening of bubble populations inside porous media
Pore-network simulation of Ostwald ripening between CO2 (red) and H2 (cyan) bubbles (depcited as circles), and their size distribution (Bueno, Ayala, Mehmani, 2023)
Ostwald ripening is the process by which isolated, partially miscible bubbles exchange mass with each other via molecular diffusion through the surrounding wetting phase. The force that drives this diffusion is the gradient in the capillary pressure of bubbles. In a bulk fluid, wherein bubbles are spherical, all bubbles merge into one big bubble due to ripening. Whereas in a porous medium, bubbles evolve towards a new distribution with different bubble shapes and sizes than their initial distribution. Such evolution dynamics become even more complicated when the initial bubble population exhibits a heterogeneous composition (e.g., CO2 and H2 in underground hydrogen storage). Our goal is to develop computational models and macroscopic theories, validated against experiments conducted by our collaborators, to understand multi-componenet Ostwald ripening and the effects it has on the hydraulic properties and storage capacity of a porous material. The implications are relevant to subsurface CO2 sequestration, underground H2 storage, and the optimal design of electrolizers and fuel cells where oxygen/water management are important design and operational considerations.
References:
Xu, Mehmani et al. (2019),
Wang, Mehmani, Xu (2021),
Mehmani & Xu (2022),
Mehmani & Xu (2022),
Yu et al. (2022),
Bueno, Ayala, Mehmani (2023)
Geomaterials characterization through multiresolution imaging
Geologic formations are often very heterogeneous. Rock properties such as permeability or Elastic moduli can vary by orders of magnitude from one location to the next. Complicating matters further, the scale at which flow and deformation occur is in the order of a few microns, which is much smaller than the meter scale where engineering decisions are made. Our goal is to bridge this gap through multiresolution imaging. We combine meter-scale measurements such as hyperspectral imaging and optics with microscale data obtained from microscopy, experiments, or simulation in order to map the spatial variability of rock properties at ultra-high resolution. Specimens that are the frequent subjects of our study are cores. The produced maps may subsequently be upscaled and used as inputs to reservoir simulators or studied in isolation to extract useful insights about the interaction between microstructure and macroscale properties. We have demonstrated the success of such an approach for a 120ft organic rich shale from the Green River formation in Utah.
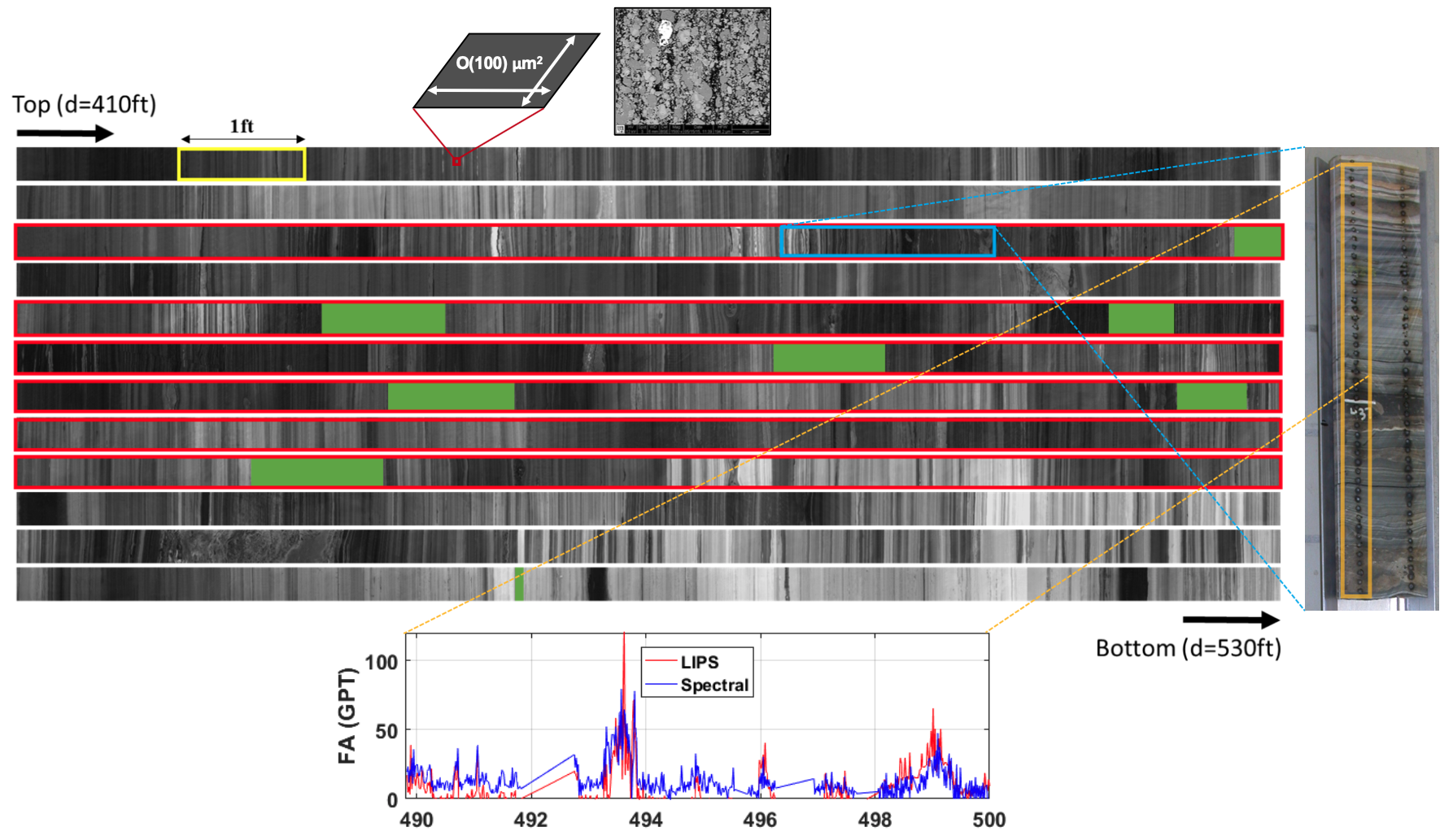
Organic content mapped at sub-millimeter resolution for a 120ft immature shale (Mehmani et al. 2016a, 2017).
Hybrid computing to bridge microscale and macroscale physics
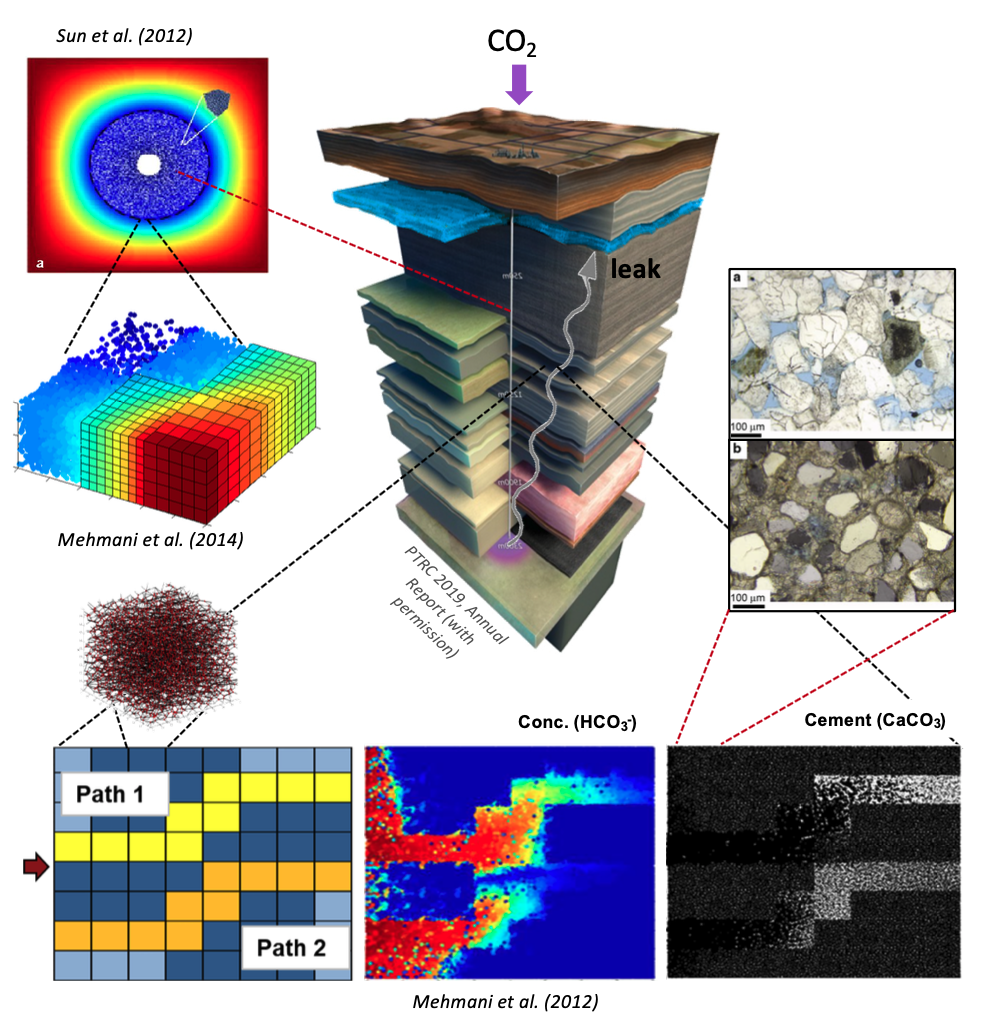
Hybrid computing for understanding the implications of CO2 leakage [center image courtesy of Petroleum Technology Research Centre’s Aquistore project].
Flow and transport in porous media occur at the microscale but have macroscopic manifestations that are of practical importance in a several engineering applications. In CO2 storage, for example, geochemical reactions can lead to mineral dissolution or precipitation that alter the microstructure of a rock and ultimately enhance or reduce its permeability. Quite often, it is desirable to model such systems purely at the macroscale without ever resolving the microscale dynamics. When this is possible, one says that scales are separated. A purely macroscale description can then be constructed and used in practice. For many practical problems, including strong mineral dissolution and precipitation, scales are not separated and the dynamics of the microscale remain coupled to those of the macroscale. In this case, a purely macroscopic description does not exist and microscale computations must be, somehow, incorporated into macroscale modeling. Such models, that establish a two-way coupling between a macroscale and a microscale model are called hybrid, and various techniques have been proposed in the literature targeting different aspects of the problem. We focus on hybrid mortar domain decomposition methods, which allow parts of a domain to be represented with a macroscale model and other parts with a microscale model. The two parts are coupled by exchanging information at the interface. The framework has the advantage of coupling fundamentally different model types, with potentially different physics, and being scalable on parallel platforms. They can also be used to simply solve very large, purely microscale problems. Together with our collaborators, we have developed and applied such techniques to passive and reactive transport in CO2 sequestration and leakage, non-Newtonian flow, and near-well as well as far-field upscaling of permeability.
References:
Mehmani et al. (2014),
Mehmani et al. (2012),
Sun, Mehmani, Balhoff (2012),
Sun, Mehmani, et al. (2012)